What the Fermions Exchange it really is?(划掉)[1]
费米子交换效应的探讨(好官方……)[2]
在 Path Integral 的架构下,交换效应比较简单的写出来;[3]
对于玻色子的配分函数:[4]
\[ N!e^{-\beta V_{Bosons}^{(N)}} = (e^{-\beta E_{ooo...}} + A_{1}^{1}C_{N}^{2}e^{-\beta E_{(0o...)}} + A_{2}^{2}C_{N}^{3}e^{-\beta E_{(O...)}} ...) \]
[5] 也可以写作迭代形式:
\[ Ne^{-\beta V_{Bosons}^{(N)}} = \sum_{k+1}^{N} e^{-\beta (E_N^{(k)} + V_{Bosons}^{(N-k)})} \] \[ E_N^{(k)} = \sum_{l=N-k+1}^{N} \sum_{j=1}^{P} E_{string}(r_{l}^{j+1}-r_{l}^{j}) \]基本就是 N-k+1 ~ N 的环的所有 String
复杂度基本上可以控制在多项式内。
对于费米子的配分函数:[6]
\[ N!e^{-\beta V_{Fermions}^{(N)}} = (e^{-\beta E_{ooo...}} - A_{1}^{1}C_{N}^{2}e^{-\beta E_{(0o...)}} + A_{2}^{2}C_{N}^{3}e^{-\beta E_{(O...)}} ...) \] [7]若是考虑合并成两个符号相反的项
则有
\[\begin{aligned} N!e^{-\beta V_{Fermions}^{(N)}} = e^{-\beta E_{ooo...}} & + A_{2}^{2}C_{N}^{3}e^{-\beta E_{(O...)}} + ... \\ - & A_{1}^{1}C_{N}^{2}e^{-\beta E_{(0o...)}} + A_{3}^{3}C_{N}^{4}e^{-\beta E_{(O...)}} + ... \end{aligned}\] [8]| [1] | 这个网站 Markdown 做不到 T_T. |
| [2] | 很学术才是吧 |
| [3] | 实际上很繁琐。(不过我比较喜欢能画图的表示方法) |
| [4] | Hirshberg, Rizzi, and Parrinello, “Path Integral Molecular Dynamics for Bosons.” 实现起来建议不要采用自调用函数形式,我的版本特别慢。 |
| [5] | 这个 O 0 o 自然是代表 三,双,单 玻色子交换的情况啦。 |
| [6] | Hirshberg, Invernizzi, and Parrinello, “Path Integral Molecular Dynamics for Fermions: Alleviating the Sign Problem with the Bogoliubov Inequality.” 实际上也有迭代的表示但和本文关系不大。 |
| [7] | 这个 O 0 o 也自然是代表 三电子,双电子,单电子 交换的情况啦。 |
| [8] | 没有什么意义但下文分析起来十分有用的一步。 |
为什么这里不能舒服地计算,原因是这个属于震荡函数的积分,非要上 Montecarlo 直接算的话(按都是正的来),就会受制于 +- 的平均符号,叫符号问题(NP hard)(而且 Markiv chain Montecarlo 的许多算法都不能准确各个局域之间的分布)。[10]
对于现存的解决方法,例如 DMC 之类,通过划分各个符号区域(试探波函数)并限制采样(产生/湮灭)来达到所取皆为正的。VMC (猛)是直接变分算的,效率(精度)低下但有效。还有其他各式各样的算法不一一在这里说了。(先挖坑)[11]
那么对于此我的理解呢,(划掉-是要温柔对待采样-划掉)是这样解释粒子的全同性:
\(fermions\) 不聚集[12]
(5) 式前几项比后几项重要
没了
那么对于几个相同自旋的 \(fermions\) 来说
(5) 式结果为正就意味着一件事:\(\begin{aligned} e^{-\beta E_{ooo...}} & + A_{2}^{2}C_{N}^{3}e^{-\beta E_{(O...)}} + ... \\ 大于 & \\ & A_{1}^{1}C_{N}^{2}e^{-\beta E_{(0o...)}} + A_{3}^{3}C_{N}^{4}e^{-\beta E_{(O...)}} + ... \end{aligned}\)
那么因为 \(fermions\) 不聚集 <1> [13],我们定义:聚集的 \(fermions\) 是同一个 \(fermions\) [14](合理 \(reasonable\))那么我们可以保证。\(\begin{aligned} e^{-\beta E_{ooo...}} > e^{-\beta E_{(0o...)}} \end{aligned}\)
因为 <1> 我们总会有 \(\begin{aligned} E_{ooo...} < E_{(0o...)} < ... \end{aligned}\)
则必定会有 <2>
在绝对零度下 \( \beta \rightarrow \infty \) 那么 \(\begin{aligned} e^{-\beta E_{ooo...}} > C_{N}^{2}e^{-\beta E_{(0o...)}} \end{aligned}\)
那么 <2> 我们的结果就必定不会为负数。
\( Q.E.D. \)[15]
...
.............
然而,为了保证计算的时候的 <1> 我们需要重新排列采样的粒子,在没有任何优化的情况下:[16]
\[ \sum_{}^{N}(\sum_{}^{P_1}...\sum_{}^{P_{beads}} E_{String}(P))\] [17]复杂度达到了惊人的 \( O( (N!b)^{b}Nb ) \) (beads & Number of Particles)
不过这是后话了(再挖一个坑)[11]
| [9] | 有理有据令人信服。 |
| [10] | 各个局域之间的分布不平衡很明显是采样不够,不过很难能达到足够的采样,推荐增强采样方法。 |
| [12] | 同种同自旋(下同)。这个我觉得应该是没什么问题的吧,毕竟是个费米子。 |
| [13] | <1> 就是 1. \(fermions\) 不聚集[12],那么聪明的你一定知道下面的…… |
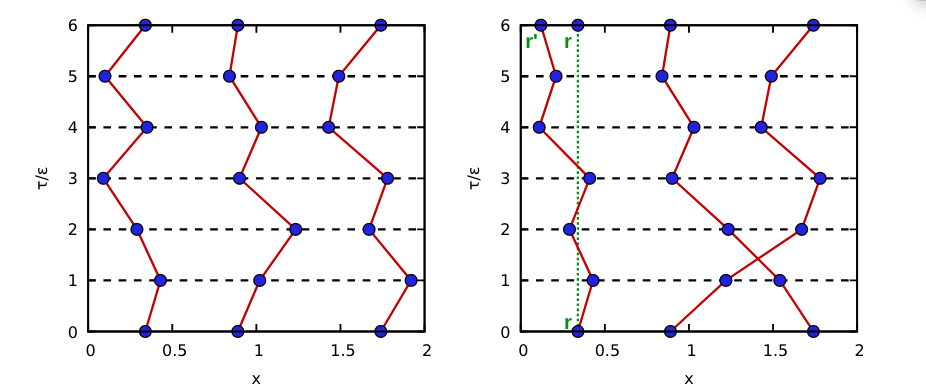
| [14] | 什么意思呢,就是在 timeslices 间分辨费米子靠的是位置远近,离得最最近就是,离得远的就不是。(不完全是这个意思,因为这个远近是从总的 path 来看的,不过也可以这样认为) |
| [15] | 我不是故意这么短的,不过毕竟越简洁越正确(误)。 |
| [16] | 那肯定有优化啊,先把 N!拿掉再说,说着掏出一个随机优化方法:是蒙特卡洛!(一片失望声,寥寥几个掌声),才怪!是梯度下降!(轻微地欢呼)利用深度学习。(场面一度热烈沸腾,难以维持秩序)。 |
| [17] | 就是遍历出来所有排列全部路径的权重。(Nb! /滑稽) |
| [11] | 写博客神清气爽,不会鸽不会鸽。 |
然而 But however
我们忽略了一点点小小的细节 :>
对于\( \frac{it}{\hbar}≝\beta\)
\[ exp\{-\frac{1}{ħ} \sum^{P}_{k} (\frac{\beta \hbar}{P} V_{x_k} + \frac{P}{\beta\hbar}\frac{m}{2} (x_{k+1}-x_k)^2) \} \]在 \( T→0\) 有极限 \( \frac{\beta \hbar}{P}→∞\) \( (7) \) 式可以化为 \( exp\{-\frac{1}{ħ} \sum^{P}_{k} \frac{\beta \hbar}{P} V_{x_k} \} \)
而 \( T→∞\) 有极限 \( \frac{\beta \hbar}{P}→0\) \( (7) \) 式可以化为 \( exp\{-\frac{1}{ħ} \sum^{P}_{k} \frac{P}{\beta\hbar}\frac{m}{2} (x_{k+1}-x_k)^2 \} \)
写为另一表述有 \( {it}≝\tau\)
\( \frac{\tau}{P}→0\) 化为 \( exp\{-\frac{1}{ħ} \sum^{P}_{k} \frac{P}{\tau}\frac{m}{2} (x_{k+1}-x_k)^2 \} \)
\( \frac{\tau}{P}→∞\) 化为 \( exp\{-\frac{1}{ħ} \sum^{P}_{k} \frac{\tau}{P} V_{x_k} \} \)
事实上可以
\[ \frac{\beta \hbar}{P} ≝ 1 \]保证了上述证明作用不被无穷小化,但有效性还有待商榷。
